今回と次回の授業では、「非線形方程式 $f(x)=0$ の解を求める」という問題を扱います。
線形方程式（一次方程式）$ax+b=0$ に対しては、解 $x=-\frac{b}{a}$ が簡単に計算できます。一方で非線形方程式に対しては、二次方程式 $ax^2+bx+c=0$ の解 $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ のように公式を用いて解を計算できる場合もありますが、一般の場合にはそれは困難です。
そこで、厳密解（厳密な意味で正しい解）ではなく、近似解（厳密解に近いある程度良い解）を求めることを考えます。
今回の授業では、方程式の近似解を求める有名なアルゴリズムの一つである二分法（bisection method）について説明し、プログラムとしての実装を行います。
連続な関数 $f:\mathbb{R}\to\mathbb{R}$ が与えられているとし、方程式 $f(x)=0$ の近似解を求めることを考えます。
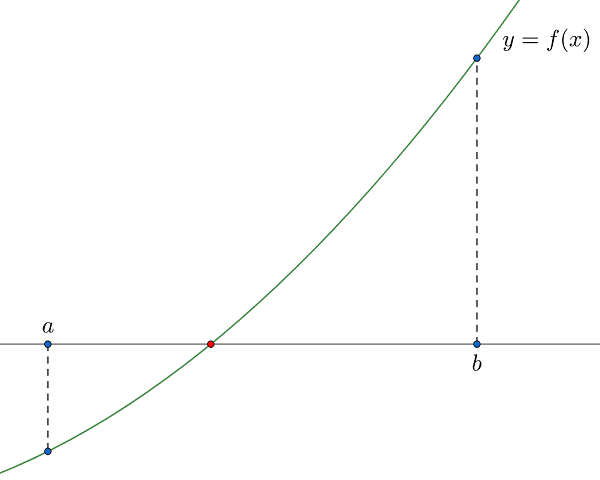
$a<b$ を満たす実数 $a, b$ を取り、$f(a)$ と $f(b)$ が異符号、すなわち $f(a)\cdot f(b)<0$ と仮定します。
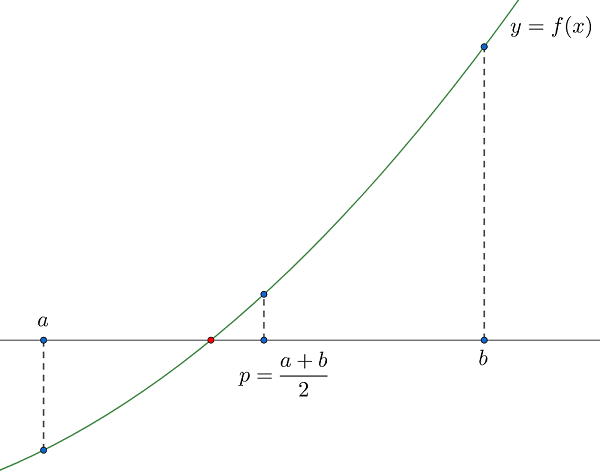
このとき、$f(a)>0$ かつ $f(b)<0$、または、$f(a)<0$ かつ $f(b)>0$ であり、関数 $f$ は連続ですので、中間値の定理によって $a$ と $b$ の間に $f(x)=0$ の解（厳密解）が少なくとも一つ存在することが保証されます。
（※実際には、関数 $f$ は区間 $[a,b]$ 上で定義されていて連続であれば十分です。）
ここで、$a$ と $b$ の中点 $p=\frac{a+b}{2}$ を考えます。もし $f(p)=0$ なら、方程式 $f(x)=0$ の厳密解 $p$ が見つかったことになります。そうでなければ、$f(p)>0$ または $f(p)<0$ です。
$f(a)$ と $f(p)$ が異符号、すなわち $f(a)\cdot f(p)<0$ の場合には、再び中間値の定理によって $a$ と $p$ の間に $f(x)=0$ の厳密解が存在することが保証されます。
$f(a)$ と $f(p)$ が同符号、すなわち $f(a)\cdot f(p)>0$ の場合には、$f(p)$ と $f(b)$ が異符号になりますので、同様に中間値の定理によって $p$ と $b$ の間に $f(x)=0$ の厳密解が存在することが保証されます。
いずれの場合も、厳密解が存在する区間の幅が半分になります。したがって、上の操作を繰り返すことにより、厳密解が存在する範囲をどんどんと狭めることができます。
最終的には、区間の幅がある一定の数値より小さくなった時点で繰り返しを終了し、区間の中点が近似解として得られます。
例として、関数 $f(x)=x^3-2$ に対して、方程式 $f(x)=0$ の区間 $[0,3]$における近似解を計算することを考えます。
まず、関数 $f$ をMATLABの関数として定義します。
function value = f(x)
value = x.^3-2; %xがベクトルの場合にも成分ごとに計算できるように「.^」を使う
end
続いて、区間 $[0,3]$ における関数 $f$ のグラフを描画してみます。
%plot --format svg
%上の行はコメントの書き方だが、Octaveにおいて出力される画像の形式を指定するという意味を持つ
%コードの一行目に書く必要がある
%グラフをきれいに表示するための「おまじない」だと思っておけばよい
x = 0:0.01:3;
y0 = x*0; %x軸を描画するために、ベクトルxと同じ長さで成分が0のベクトルy0を作る
y = f(x); %ベクトルxの成分ごとに関数fの値を計算してベクトルyを作る
plot(x,y0,"b-") %x軸を描画する
grid on %グリッド線を表示する（plotより後に書く必要がある）
hold on %複数のplotを一つの図に表示する（デフォルトのoffだと最後のplotだけが有効になる）
plot(x,y,"r-") %関数fのグラフを描画する
$a=0$、$b=3$ とすると、$f(a)<0$ かつ $f(b)>0$ ですので、二分法を使用することができます。
$a$ と $b$ の中点を $p=\frac{a+b}{2}$ として、$f(a)\cdot f(p)$ の値を計算します。
a = 0;
b = 3;
p = (a+b)/2;
printf("a=%f, b=%f, b-a=%f, p=%f, f(p)=%f, f(a)*f(p)=%f\n",a,b,b-a,p,f(p),f(a)*f(p))
a=0.000000, b=3.000000, b-a=3.000000, p=1.500000, f(p)=1.375000, f(a)*f(p)=-2.750000
$f(a)\cdot f(p)<0$ ですので、$a$ と $p$ の間に厳密解が存在することが分かり、改めて $b=p$ とおきます。再び $p=\frac{a+b}{2}$ として、$f(a)\cdot f(p)$ の値を計算します。
b = p;
p = (a+b)/2;
printf("a=%f, b=%f, b-a=%f, p=%f, f(p)=%f, f(a)*f(p)=%f\n",a,b,b-a,p,f(p),f(a)*f(p))
a=0.000000, b=1.500000, b-a=1.500000, p=0.750000, f(p)=-1.578125, f(a)*f(p)=3.156250
$f(a)\cdot f(p)>0$ ですので、$p$ と $b$ の間に厳密解が存在することが分かり、改めて $a=p$ とおきます。再び $p=\frac{a+b}{2}$ として、$f(a)\cdot f(p)$ の値を計算します。
a = p;
p = (a+b)/2;
printf("a=%f, b=%f, b-a=%f, p=%f, f(p)=%f, f(a)*f(p)=%f\n",a,b,b-a,p,f(p),f(a)*f(p))
a=0.750000, b=1.500000, b-a=0.750000, p=1.125000, f(p)=-0.576172, f(a)*f(p)=0.909271
$b-a<0.02$ となるまで、上記の操作を手動で繰り返し行ってください。「手動で行う」演習ですので、if文、for文、while文を使わないこと。Markdownとして説明を付ける必要はなく、コードのみを書けばよいです。
%演習1のコード
function value = f(x)
value = x.^3-2;
end
a = 0;
b = 3;
p = (a+b)/2;
printf("a=%f, b=%f, b-a=%f, p=%f, f(p)=%f, f(a)*f(p)=%f\n",a,b,b-a,p,f(p),f(a)*f(p))
b = p;
p = (a+b)/2;
printf("a=%f, b=%f, b-a=%f, p=%f, f(p)=%f, f(a)*f(p)=%f\n",a,b,b-a,p,f(p),f(a)*f(p))
a = p;
p = (a+b)/2;
printf("a=%f, b=%f, b-a=%f, p=%f, f(p)=%f, f(a)*f(p)=%f\n",a,b,b-a,p,f(p),f(a)*f(p))
%ここに、コードの続きを書いてください
a=0.000000, b=3.000000, b-a=3.000000, p=1.500000, f(p)=1.375000, f(a)*f(p)=-2.750000 a=0.000000, b=1.500000, b-a=1.500000, p=0.750000, f(p)=-1.578125, f(a)*f(p)=3.156250 a=0.750000, b=1.500000, b-a=0.750000, p=1.125000, f(p)=-0.576172, f(a)*f(p)=0.909271
二分法のアルゴリズムは、次のようにまとめられます。
入力：関数$f$、区間の両端 $a$ と $b$、許容誤差 $TOL$（tolerance errorに由来）
出力：反復回数 $n$、近似解 $p$
Step 1：関数 $f$ を定義する。$a$、$b$、$TOL$を初期化する。$n=0$ とする。
Step 2：$b-a\geq 2\cdot TOL$ の間、次のStep 2-1～2-3を繰り返す。
Step 2-1：$n$ に $1$ を加算する。
Step 2-2：$p=\frac{a+b}{2}$ とする。
Step 2-3：もし $f(a)\cdot f(p)<0$ なら、$b=p$ とする。そうでなければ、$a=p$ とする。
Step 3：$p=\frac{a+b}{2}$ とする。
Step 4：反復回数 $n$ と近似解 $p$ を出力する。
上記のアルゴリズムにおいて反復の終了条件となっているのは、$b-a<2\cdot TOL$ です。反復の終了後には厳密解が区間 $[a,b]$ の中にあることが保証されており、かつ近似解は区間の中点 $\frac{a+b}{2}$ ですので、終了条件の不等式から近似解と厳密解の誤差が $TOL$ より小さいことが分かります。
Step 2では、$f(p)==0$ の場合に厳密解 $p$ が求まったとして反復を終了することもできますが、小数の計算には誤差が含まれるため $f(p)==0$ を正しく判定することは困難です（$\varepsilon$ を小さな数として、$|f(p)|<\varepsilon$ で判定する手段はあります）。$f(p)==0$ の場合に $a=p$ として反復を続けてもアルゴリズム上の問題は生じないため、上記ではそのようにしています。
反復回数の上限 $N$ を予め設定しておいて、追加の終了条件として $n>N$ を使うという考え方もあります。
上記の二分法のアルゴリズムを実現するコードを書き、関数 $f(x)=x^3-2$ に対して方程式 $f(x)=0$ の区間 $[0,3]$における近似解を求めてください。ただし、許容誤差 $TOL=0.00001$ とします。
%演習2のコード
function value = f(x)
value = x.^3-2;
end
a = 0;
b = 3;
TOL = 0.00001;
n = 0;
%ここに、コードの残りを書いてください
p = (a+b)/2;
printf("反復回数n=%d, 近似解p=%f\n",n,p)
反復回数n=0, 近似解p=1.500000
二分法のアルゴリズムにおける区間の両端の初期値 $a$ と $b$、許容誤差 $TOL$、反復回数 $n$ の関係について考察してください。Markdownのセルに解答を書いてください。
（演習3の解答）
二分法のアルゴリズムにおいて、計算量の観点から関数 $f$ の値の計算回数は最小限に抑えるべきです。$f(a)$ の値を格納する変数 $fa$ と $f(p)$ の値を格納する変数 $fp$ を新たに用いることで、演習2のコードを改良してください。
%演習4のコード
演習1～演習4に取り組んでください。