1.1. ニュートン法の考え方¶
微分可能な関数 $f:\mathbb{R}\to\mathbb{R}$ が与えられているとし、方程式 $f(x)=0$ の近似解を求めることを考えます。
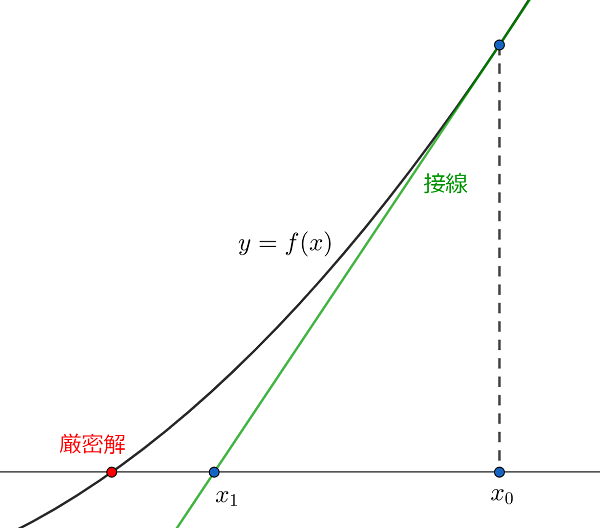
初期値として、厳密解に近いと思われる値 $x_0$ を一つ取ります。
$x$-$y$ 平面上で曲線 $y=f(x)$ の点 $(x_0,f(x_0))$ における接線を考え、その $x$ 切片($x$ 軸との交点の $x$ 座標)を $x_1$ とします。ここで、考えている接線の方程式は
$$ y=f'(x_0)(x-x_0)+f(x_0) $$であるため、点 $(x_1,0)$ を代入することで
$$ x_1=x_0-\frac{f(x_0)}{f'(x_0)} $$が得られます。多くの場合に、$x_1$ は $x_0$ よりも厳密解に近い値となります。